TSP (Traveling Salesman Problem)
TSP는 모든 도시들을 한번씩 방문하고 원래 시작점으로 돌아오는
최단 경로의 이동 순서를 구하는 것이다.
Excel에서도 이 문제를 간단하게 풀 수 있는데
해찾기 추가 기능을 이용하면 된다.
해찾기 추가 기능은 수동으로 추가해야 사용할 수 있다.
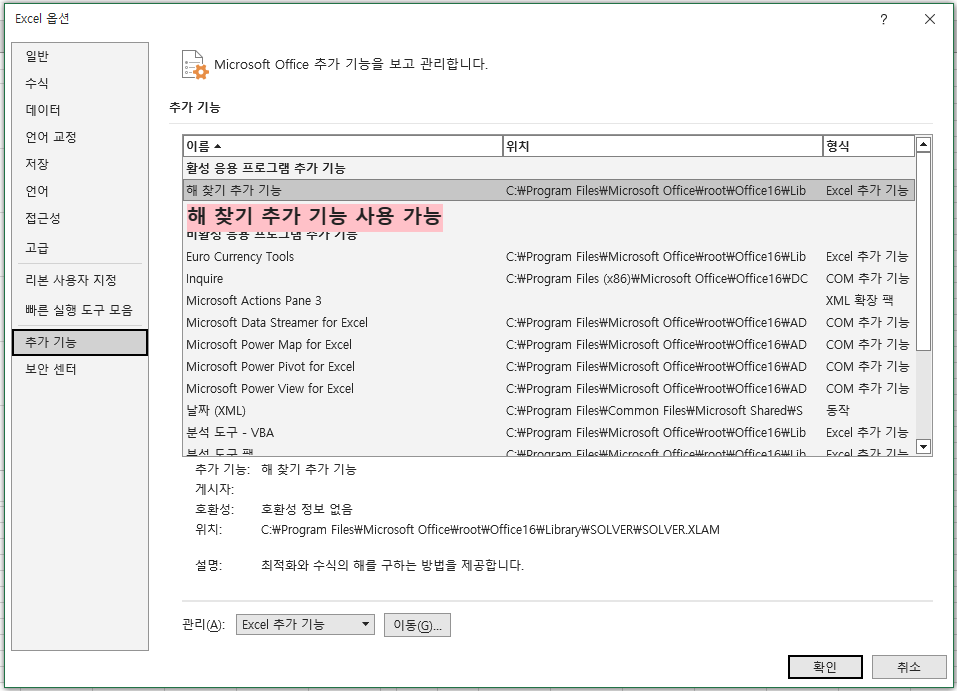
Excel 옵션의 추가 기능 창 하단의 관리에서
Excel 추가 기능을 선택하고 이동 버튼을 누르면

추가 기능 창이 나타난다.
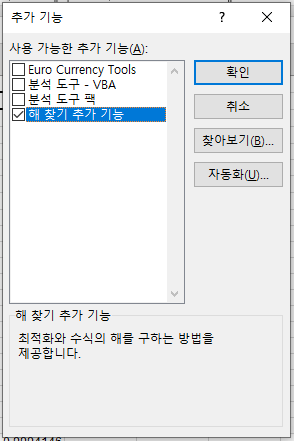
해 찾기 추가 기능을 체크하고 확인 버튼을 누르면
다음과 같이 해 찾기 추가 기능을 사용할 수 있게 된다.
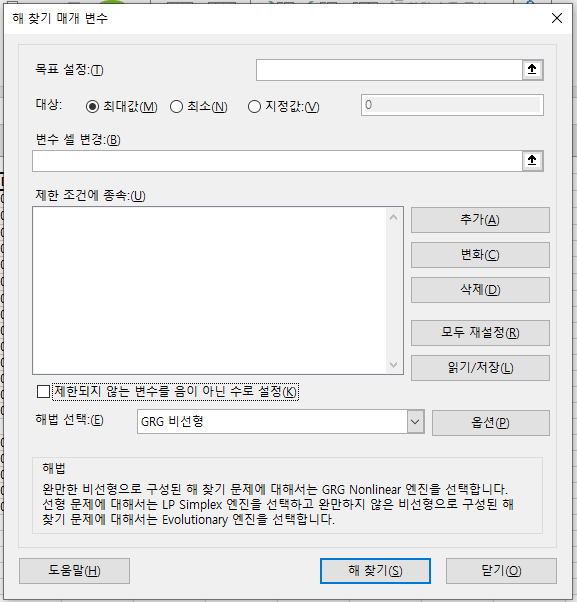
리본 메뉴의 [데이터] 탭 오른쪽 가장자리에 [해 찾기] 버튼이 생겼다.

해 찾기 버튼을 눌러서 다음과 같은 창이 나타나면 성공이다.
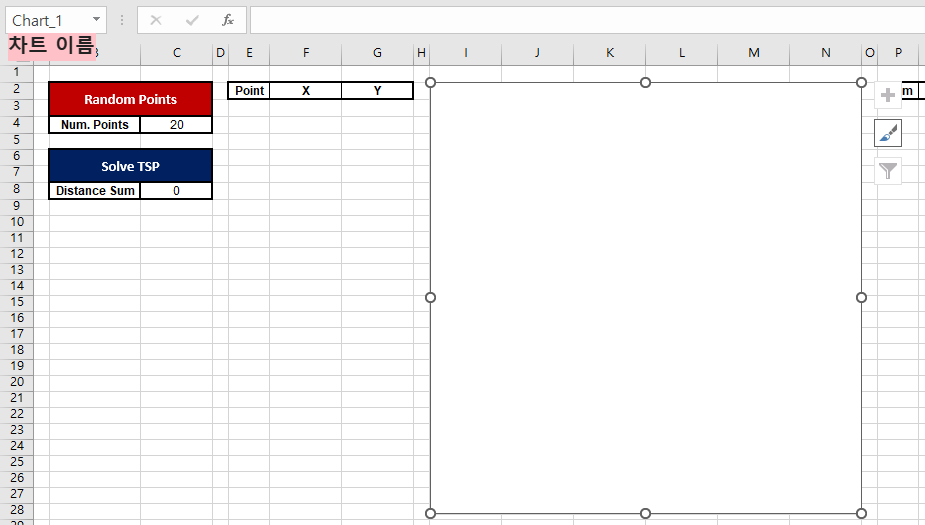
이제 시트에 다음과 같이 입력하고
빨간 버튼의 이름은 Random_Points
파란 버튼의 이름은 Solve_TSP 라고 정한다.
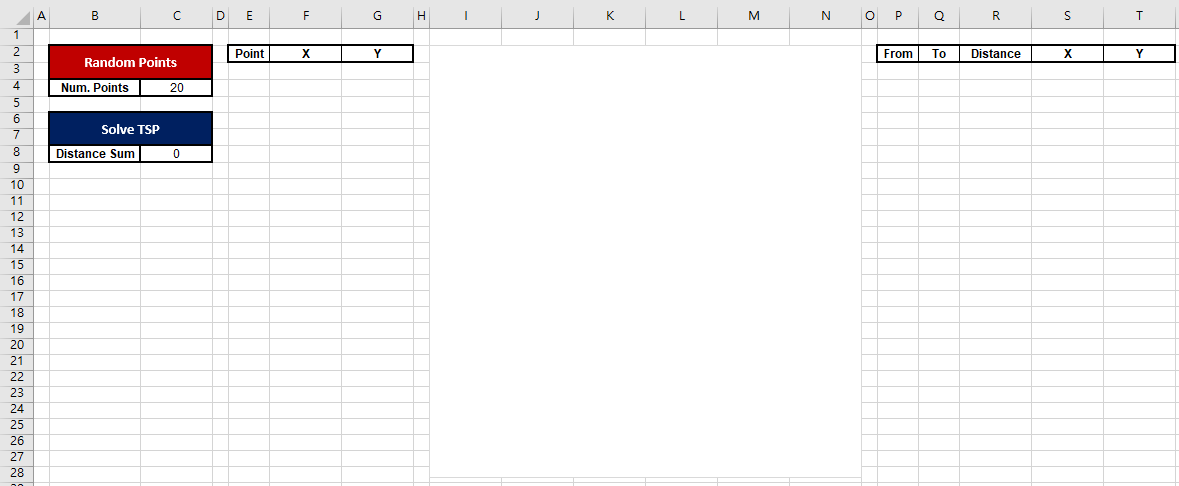
가운데에는 직선 및 표식이 있는 분산형 차트를 넣고
차트의 이름은 Chart_1 이라고 정한다.
빨간 버튼에 다음 코드를 연결한다.
Sub Random_Points_Click()
Dim i As Long
Dim Num_Points As Long
Dim rng1 As Range
Num_Points = [C4]
[E3:G12] = ""
[P3:T102] = ""
[C8] = "=SUM(R3:R" & Num_Points + 2 & ")"
Application.Calculation = xlCalculationManual
For i = 0 To Num_Points - 1
Cells(i + 3, 5) = i
Cells(i + 3, 6) = Rnd
Cells(i + 3, 7) = Rnd
Cells(i + 3, 16) = i
Cells(i + 3, 17) = "=P" & i + 4
Cells(i + 3, 18) = "=((OFFSET($F$3,P" & i + 3 & ",0)-OFFSET($F$3,Q" & i + 3 & ",0))^2+(OFFSET($G$3,P" & i + 3 & ",0)-OFFSET($G$3,Q" & i + 3 & ",0))^2)^0.5"
Cells(i + 3, 19) = "=OFFSET($F$3,P" & i + 3 & ",0)"
Cells(i + 3, 20) = "=OFFSET($G$3,P" & i + 3 & ",0)"
Next i
Cells(Num_Points + 3, 19) = [S3]
Cells(Num_Points + 3, 20) = [T3]
Application.Calculation = xlCalculationAutomatic
Set rng1 = Range(Cells(3, 19), Cells(3 + Num_Points, 20))
ActiveSheet.ChartObjects("Chart_1").Activate
With ActiveChart
.SetSourceData Source:=rng1
.FullSeriesCollection(1).ApplyDataLabels Type:=xlDataLabelsShowLabel
.FullSeriesCollection(1).DataLabels.Format.TextFrame2.TextRange.InsertChartField msoChartFieldRange, "=Sheet1!$P$3:$P$" & Num_Points + 2, 0
.FullSeriesCollection(1).DataLabels.ShowCategoryName = False
.FullSeriesCollection(1).HasLeaderLines = False
End With
[A1].Select
End Sub
파란 버튼에 다음 코드를 연결한다.
Sub Solve_TSP_Click()
Dim Num_Points As Long
Num_Points = [C4]
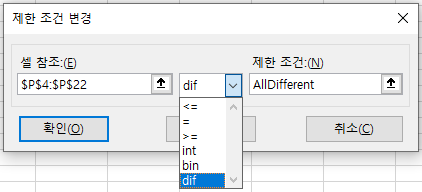
SolverAdd CellRef:="$P$4:$P$" & Num_Points + 2, Relation:=6, FormulaText:="AllDifferent"
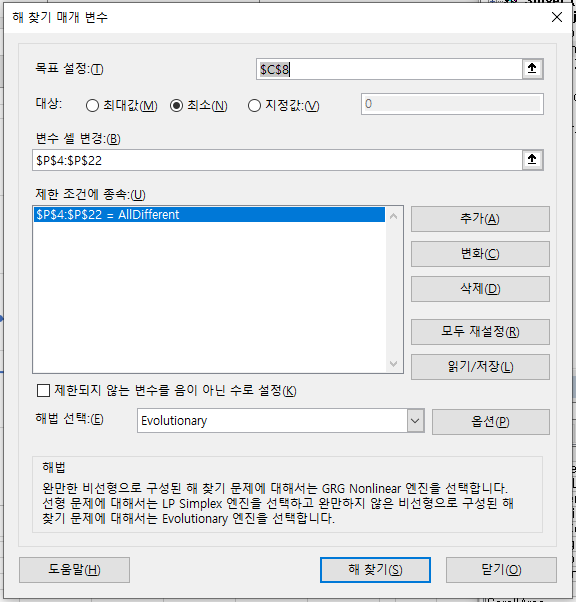
SolverOk SetCell:="$C$8", MaxMinVal:=2, ValueOf:=0, ByChange:="$P$4:$P$" & Num_Points + 2, _
Engine:=3, EngineDesc:="Evolutionary"
SolverSolve
SolverDelete CellRef:="$P$4:$P$" & Num_Points + 2, Relation:=6, FormulaText:="AllDifferent"
End Sub
위 코드에서 Relation:=6 이란 dif 를 의미한다.
드롭다운 메뉴에서 6번째에 있어서 6이다.
해 찾기 매개 변수 창에 입력된 값과 Solve_TSP_Click() 을 비교해보면
각 코드가 무엇을 의미하는지 알 수 있다.
그리고 하나 더 해야할 것이 있다.
VBA Editor 창의 [도구] - [참조] 를 선택하고
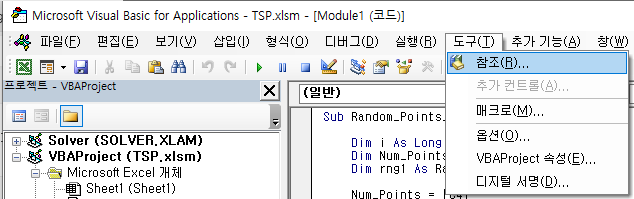
Solver 에 체크를 하고 확인을 누르면
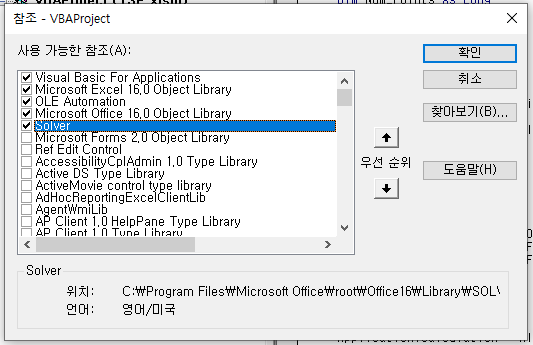
프로젝트 탐색기에 참조 대상SOLVER.XLAM 이 생긴다.
해 찾기 기능을 사용하기 위해 이게 있어야 VBA 코드를 실행할 수 있다.
이제 빨간 버튼을 눌러 무작위로 점을 생성해보자.
생성할 점의 갯수는 C4 Cell에 입력하면 된다.
너무 큰 숫자를 입력하면 계산하는데 오랜 시간이 걸리니까
적당히 20개 수준에서 조절하자.
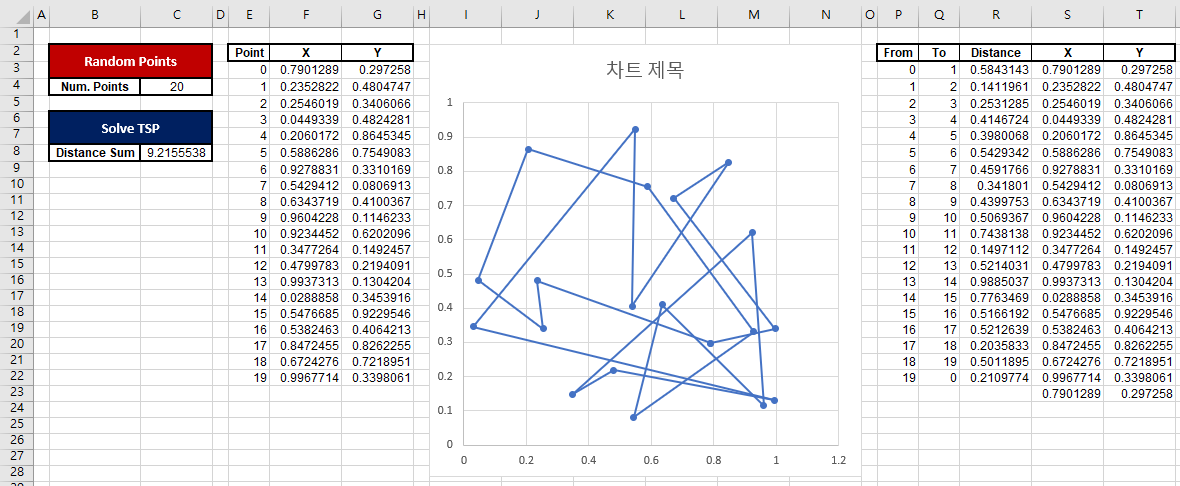
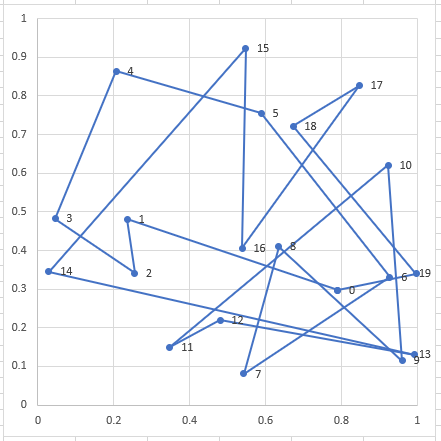
차트에 찍힌 점이 직선으로 연결되어 있다.
차트 제목이 거슬리니까 지워버리고
가로, 세로축의 범위를 0~1로 고정한다.
그리고 데이터 레이블 추가를 해서
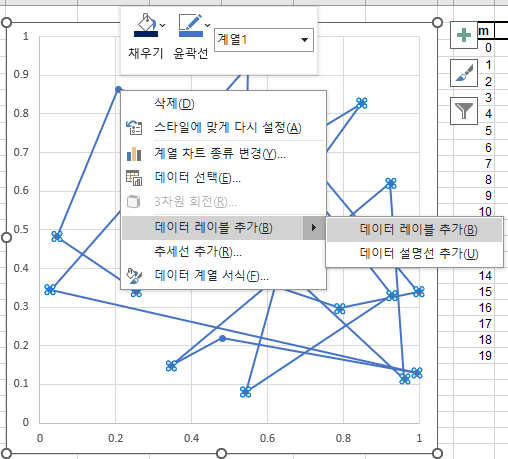
데이터 레이블 서식에서
Y 값을 체크 해제하고, 셀 값을 체크하면

차트의 점마다 번호가 생긴다.
E 컬럼의 번호다.
이제 파란 버튼을 실행하면 되는데
실행하고 0.1초만에 다음과 같은 창이 나타난다.
얼마 풀지도 않았으니, 계속을 눌러보자.
Excel 창 왼쪽 하단에 글자가 빠르게 점멸하면서
뭔가 열심히 계산하는 것이 보인다.
기다리다 지루해서 Esc 키를 누르면
조금 전에 봤던 것과 비슷한 창이 나타나는데
지루해서 그만 계산하라고 Esc 키를 눌렀으니
정지를 선택하자.
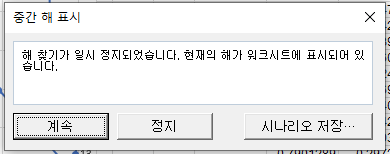
그러면 사용자에 의해 중단되었다는 창이 나타나고
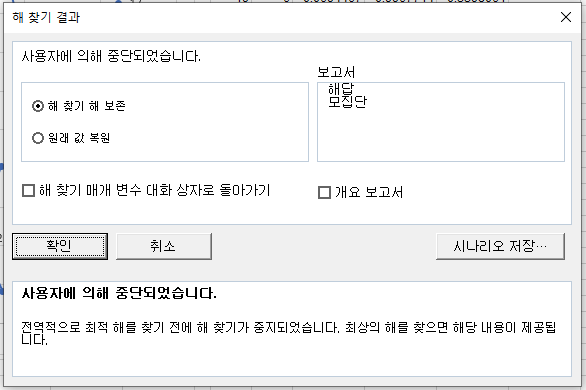
계산이 끝날 때까지 기다리면 다음과 같은 창이 나타날 것이다.
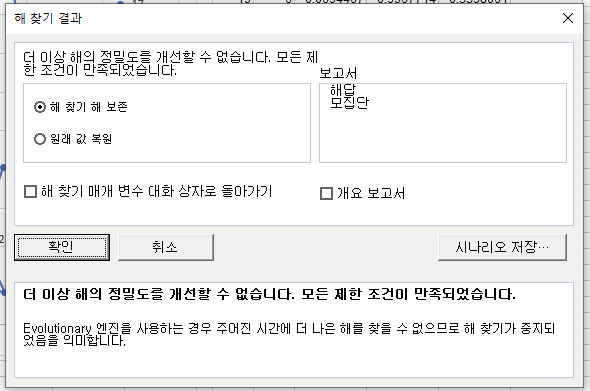
어느 경우라도 해 찾기 해 보존을 선택한 후 확인을 누른다.
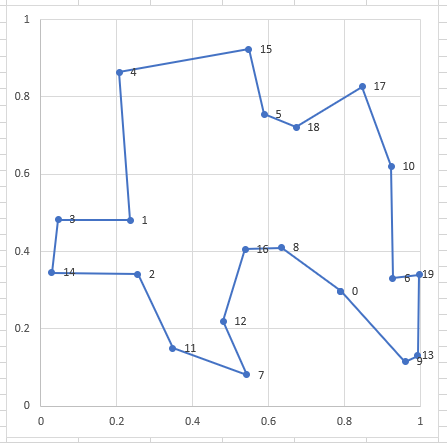
최단경로를 잘 찾은 것을 볼 수 있다.
'Excel VBA 응용' 카테고리의 다른 글
| Factorial 계산하기 (0) | 2023.12.03 |
|---|---|
| Plot Digitizer (0) | 2023.12.02 |
| Stop Watch (0) | 2023.11.29 |
| 소인수분해 (0) | 2023.11.29 |
| 콜라츠 추측 (0) | 2023.11.29 |